|
|
|
|
|
|
|
|
|
|
|
|
Derailleur allowances are the amount of extra chain required to go around a derailleur rear gearchange mechanism.
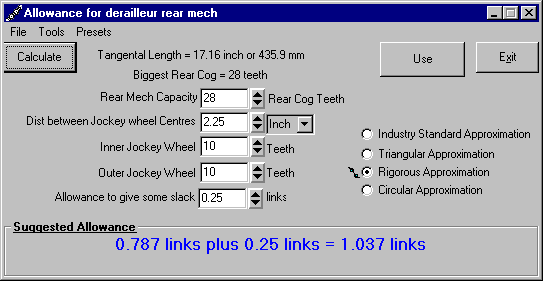
The Machinehead Chain Length Calculator has this handy pop up derailleur allowance calculator to calculate extra length of chain in a way that takes the most important dimensions of the rear mech into account:
A widely accepted approximation for the amount of extra chain required to go around a derailleur rear mech is "Add an inch/link". And its not a bad approximation for most of the rear mechs commonly in use i.e. 10 teeth on each cog/pulley/jockey wheel and about 2 1/4 to 3 3/4 inch between jockey wheel centres. But the size of the jockey wheels can vary. I have seen some with 13T inner and 15T outer wheels so an inch must surely be an under estimate for these.
|
The extra amount of chain required is approximately a bit more than the difference between the length of the red zigzag line from A to B to C to D and the blue straight length from A to D. So a simple solution can be found by resolving three triangles. It will always under estimate very slightly because the reality is the chain follows a curved path around the jockey wheels. But it will suggest bigger allowances for rear mechs with bigger jockey wheels. Even calculating the straight bits and curved bits separately this would still be effectively as tight as possible which is still too tight. So another rule of thumb is to add a small allowance to give some slack - 1/4 to 1/2 a link ought to be about right. |
The Rigorous Approximation
|
The Circular Approximation
|
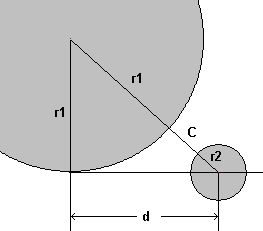
To accurately fix the position of the inner derailleur jockey wheel and the tangential point on the biggest freewheel/cassette cog ChainLengthCalc needs to know about the minimum clearance (C) when using the biggest rear cog that the rear mech was designed to handle (Rear Mech Capacity). Theoretically C can be zero because r1 and r2 are distances to chain pin centres. But in practice some clearance is desirable i.e. a bit more than zero.
By default Chainlengthcalc assumes that C = 0.1"
This value has been arbitrarily plucked out of the ether because is seems about right. It is a bit more than the difference between the radius of a 32T cog and a 31T cog. When better information becomes availiable the value of this constant can be refined by opening the file ChainLengthCalc.ini in notepad and adding an entry JW2RC Clearance=?? in the [frmRearMech] section. The following changes 'C' to 0.01":
If the capacity of your derailleur is bigger than the number of teeth on the biggest rear cog, the distance C increases by the difference between the radius of the actual cog used and the radius that the biggest cog could be. Thus any small error due to inaccuracy in the C value do not become exaggerated. Both the triangular and rigorous approximations determine the jockey wheel position and the length 'd' in this way. |
The Scale Drawing And Bit Of String ApproximationIf you haven't got a computer, abacus, slide rule, calculator etc but you have got a pair of compasses and a set square. An adequate estimate of the extra chain can be made by producing a scale drawing and wrapping a piece of string around the chain path. Click here for a table of radius values in inches for different cog sizes for 1/2 inch pitch bicycle chain. When you have finished with the string you can always use it to suspend a weather prediction cone. |
Bicycle Software | Miscellaneous Downloads | F.A.Q. | Complaints
| Page Design by Nigel Jones and the Machinehead Programming Team | Machinehead Software |